I have a new preprint on the arxiv, joint with Emily Stark. We provide the first known examples of one-ended hyperbolic groups which are not abstractly coHopfian. That means that there is a one ended hyperbolic group \(G\) which contains a finite index subgroup \(G’ \leq G \) that embeds \( G’ \rightarrow G\) as an infinite index subgroup. I encourage you to look at the paper for details. The main example and proof can be drawn out on a single side of A4 — it’s a simple surface amalgam and we exploit the tremendous flexibility you have when you take a finite cover of a surface with boundary.
We use the following Lemma extensively. It’s from Walter Neumann’s 2001 paper Immersed and virtually embedded \(\pi_1\)-injective surfaces in 3-manifolds, although, as he says, it is apparently “well known”.

The utility of this Lemma is that it reassures you that if you can imagine your desired cover — such as the following I’ve drawn below — and it satisfies a basic necessary Euler characteristic computations, then the cover does in fact exist.

For our main example you can compute your desired covers by hand, but it is worth knowing what kind of covers of a surface with boundary you can take. This lemma tells you exactly how much control you have. And mathematical research, like all forms of insecurity, is really all about control.
The proof given above is brief, to say the least, so I think it is worth expanding on the details.
First, we remind ourselves how you might construct such a cover by hand. Take a surface with genus one and a single boundary component. From a group theoretic point of view this is just the free group generated by two element \( \mathbb{F}_2 = \langle x, y \rangle \) bundled together with the conjugacy class of the commutator \( [x,y] \). For me at least, finding finite index subgroups of the free group boils down to futzing around with graphs. Thus, we let \(X\) be a bouquet of two circles and let \(\langle x,y \rangle = \pi_1X\).

On the right I drew the surfaces with boundary and on the left I drew the corresponding graphs with the loop corresponding to the boundary. Once you have drawn the graphs out it’s easy to verify that you have the boundary components you want. The trick is knowing you can find the desired finite covers. The key insight is that \(\alpha\)-sheeted covers of a graph \(X\) are in a correspondence with representations into the permutation group on \(n\) elements: \( \pi_1 X \rightarrow \textrm{Sym}(\alpha) \)
We can see how this correspondence works in practice in the example I just drew:

Giving each of vertex a number we can see that the edges labelled by a given generator of our free group gives a permutation. In this example the generator \(x\) gives the permutation \((1,2)(3)\) (see the red edges on the right), while the generator \(y\) gives the permutation \((1,2,3)\) (see the blue edges on the left). Thus we have a homomorphism determined by mapping the generators to the corresponding permutation.
At this point we need to be careful because there are some left-right issues hidden here. When I multiply group elements \(xy\) I am composing paths in the fundamental group. That means I concatenate the corresponding paths, starting with the \(x\) path and then following it with the \(y\) path. I’m reading the composition from left to right. In contrast, when I usually compose a pair of permutations \(\sigma_1 \sigma_2\) I compute the composition by reading them from right to left. But in order to be able to interpret my homomorphism correctly I’m going to have to compose my permutations in reverse order, from left to right.
Now we can compute the image of the element corresponding to the boundary curve: $$ xyx^{-1}y^{-1} \mapsto (1,2) \circ (1,2,3) \circ (1,2) \circ (3,2,1) = (1,2,3).$$ Tracing out how the boundary curve lifts is equivalent to computing this permutation element. This makes it clear that there is a single boundary component covering the previous with degree 3. (In this example it doesn’t matter in which direction we composed the permutations).
Conversely, choosing pair of permutions, say, $$(1,2)(3,4)\textrm{, and } (2,4,3) \in \textrm{Sym(4)}$$ to be the images of \(x\) and \(y\) we can construct a corresponding cover by taking 4 vertices and adding the appropriate labelled edges:

Now when we compute (remembering to compose our permutations from left to right) the image of our commutator element we get $$ xyx^{-1}y^{-1} \mapsto (1,2)(3,4) \circ (2,4,3) \circ (1,2)(3,4) \circ (3,4,2) = (1,4)(2,3).$$ Thus the surface has two boundary components, each covering the boundary in the base surface with degree two.
The take away from this discussion is that finding suitable covers corresponds to finding a suitable homomorphism $$\phi : \pi_1 X \rightarrow \textrm{Sym($\alpha$)}$$ such that the image of the elements corresponding to boundary curves are permutaions with the desired decomposition into cycles. Our weapon of choice is the fact that any even permutation can be written as the commutator of an \(\alpha\)-cycle and an involution:
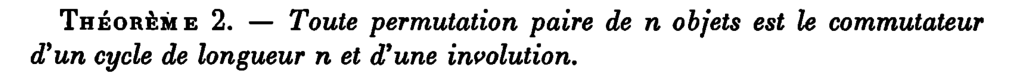
First we consider the case where \(\Sigma\) has a single boundary component. So \(\Sigma\) is a surface with genus \(g\), Euler characteristic $$ \chi(\Sigma) = 2 – 2g – |\partial \Sigma | $$ and a single boundary component, so \(|\partial \Sigma | = 1\). This corresponds to the free group generated by \(2g\) elements and the group element corresponding to the boundary, which is the product of commutators: $$( \langle x_1, y_1, \ldots x_g, y_g \rangle, [x_1,y_1]\cdots [x_g, y_g] ).$$
Suppose we wish to construct a cover of degree \(\alpha\) with the boundary components of degrees \(\alpha_1, \ldots, \alpha_k\). Then apply the above Theorem to the permutation $$\sigma = (1, \ldots, \alpha_1)(\alpha_1 +1, \ldots, \alpha_1 + \alpha_2) \cdots (\alpha_1 + \cdots + \alpha_{k-1} +1, \ldots, \alpha).$$ The theorem only applies if \(\sigma\) is an even permutation, which we compute to be equivalent to $$ \sum_i (\alpha_i -1) = \alpha – k$$ being even. As \(\chi(\Sigma) = 1-2g\) this is equivalent to \(k\) having the same parity as \(\alpha\chi(\Sigma)\), the sufficient condition given in the statement of our theorem.
Thus there exists permutations \( \sigma_x, \sigma_y \in \textrm{Sym}(\alpha)\) such that \( [\sigma_x, \sigma_y] = \sigma \). The homomorphism $$ \phi: \pi_1 \Sigma \rightarrow \textrm{Sym($\alpha$)}$$ given by mapping \(x\) to \(\sigma_x\) and \(y\) to \(\sigma_y\) therefore corresponds to a cover with the desired boundary.
Now we consider the slightly trickier general case where we have multiple boundary components, which is to say \(|\partial \Sigma| = b\). In which case the pair \((\Sigma, \partial \Sigma)\) corresponds to $$ (\langle x_1, y_1, \ldots, x_g, y_g, t_1, \ldots t_{b-1} \rangle , \{t_1,\ldots, t_{b-1}, t_{b-1}\cdots t_{1}[x_1,y_1] \cdots[x_n,y_n] \} ).$$
Now suppose we desire that the \(i\)-th boundary component is covered with degrees \(\alpha_1^i, \ldots, \alpha_{k_i}^i\), then let $$ \sigma_i = (1, \ldots, \alpha_1^i)(\alpha_1^i +1, \ldots, \alpha_1^i + \alpha_2^i) \cdots (\alpha_1^i + \cdots + \alpha_{k_i-1}^i +1, \ldots, \alpha)$$ for \(1 \leq i \leq b\). Now we wish to find \(\sigma_x, \sigma_y\) such that $$[\sigma_x, \sigma_y] = \sigma_1 \cdots \sigma_b.$$ This requires that the product of the \(\sigma_i\) is even. This means that the sum $$ \sum_i \sum_j (\alpha_j^i – 1) = \sum_i (\alpha – k_i) =\alpha b – \sum_i k_i = \alpha (\chi(\Sigma) -2 + 2g) – \sum_i k_i$$ should be even, which is true precisely when the total number of prescribed boundary components \(\sum_i k_i\) has the same parity as \(\alpha \chi(\Sigma)\).
Given that our parity condition is satisfied, we define our homormorphism \(\pi_1 \Sigma \rightarrow \textrm{Sym}(\alpha)\) as follows:
$$\begin{align} x_1 \mapsto & \sigma_x \\ y_1 \mapsto & \sigma_y \\ x_2 \mapsto & 1 \\ \vdots \\ y_g \mapsto & 1 \\ t_1 \mapsto & \sigma_1^{-1} \\ t_2 \mapsto & \sigma_2^{-1} \\ \vdots \\ t_{b-1} \mapsto & \sigma_{b-1}^{-1} \end{align} $$
Then it only remains to verify that $$ t_{b-1}\cdots t_{1} [x_1,x_2] \cdots [x_g, y_g] \mapsto \sigma_{b-1}^{-1} \cdots \sigma_1^{-1} [\sigma_x, \sigma_y] = \sigma_{b-1}^{-1} \cdots \sigma_1^{-1} \sigma_1 \cdots \sigma_{b-1} \sigma_b = \sigma_b $$ and conclude this gives us our desired cover.
QED.
(I’d like to thank Emily for informing me about Neumann’s Lemma, and Nir for various discussions related to this.)